AMO Grade 8 – Tuyển chọn câu hỏi AMO – Lớp 8

AMO Grade 8

Week 1

Answer the questions

(1) The number of days left in the month of April are 8 more than the number of days already passed. How many days are left in the month?

(2) There are 5 books belonging to 5 students. The books were put into a box, and each student pulls out an book one after the other. What is the probability that each student gets his or her own book?

(3) If diagonal of a rhombus are in ratio 5:4, and its area is 90 cm². Find the larger diagonal of the rhombus.

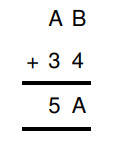
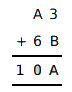
(4) Find the value of A and B, from following summation.

(5) If N = 111111², find the 6th digit in the expansion of N from the right.

(6) Eva can complete some work in 24 days, while Dylan can complete the same work in 12 days. They started the work together, and when the work was half complete, Dylan fell ill and Eva had to finish the remaining work. How long did it take to complete the work?

(7) We draw a square inside a rectangle. The ratio of the rectangle’s width the square’s side is 4:1, and the ratio of the rectangle’s length to its width is 4:1. What percentage of the rectangle’s area is inside the square?

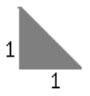
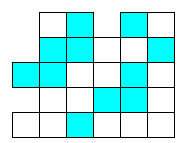
(8) How many can

fit in the shape given below?

(9)

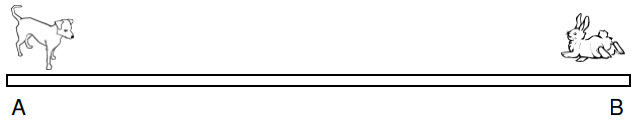
If dog can walk from A to B in 40 minutes, while rabbit can walk from B to A in 24 minutes. If both start walking at same time, after what time will they cross each other?

(10) Due to 10% discount offered by a shop, price of a shirt reduces by $ 450. Find the discounted price of shirt.

(11) If f(x) = 3 x – 5 and f(a) = 4, find the value of a.

(12) Pointing towards a girl playing cricket, Aidan says, “Her mother is the only daughter of my mother inlaw”. How is the girl related to Aidan?

(13) The number 126 is divided into two parts in the ratio 7:11. Find the absolute difference between the two parts.

(14) Simplify (a^-2 + b^-2)^-1
.
(15) In a month of 31 days, it is Monday on a given date of the month. Find the day on the same date of the next month.

Week 2

Choose correct answer(s) from the given choices

(1) Find the next number in the sequence.

7, 8, 9, 13, 14, 15, 19, 20, 21, ….

a. 22           b. 26           c. 24              d. 25

(2) How many months in a year have exactly 31 days?

a. 9            b. 5          c. 7                d. 6

(3) A frog has fallen into a ditch which is 12 meter deep. Each day the frog climbs 4 meter and than falls back by 2 meter. In how many days will the frog reach the top?

a. 4          b. 7        c. 5            d. 6

Fill in the blanks

(4) Dylan buys 1050 kilograms of eggplant from a farm at a price of $15.04 per kg. However, during his travel to the market he finds 6% of the eggplant have spoiled. If he now sells each kilogram of eggplant at $16.96, his profit percentage would be ………. %.

(5) Using the rule between IN and OUT, fill the missing number.

IN	29	13	10	22	22	16
OUT	174	91	80	…….	220	176

Answer the questions

(6) There are three possible modes of transportation in a state. We can travel by rail, by river, or by road. The state has 5000 km of rail, 15200 km of river, and 20200 km of road. Taking the three ratios (distance covered by the networks of rail:river, river:road, and rail:road), what is the value of the highest consequent?

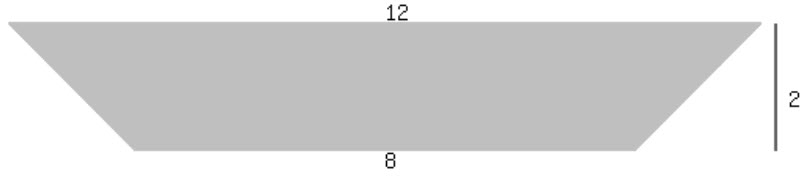
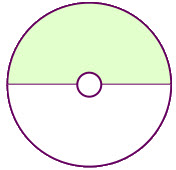
(7) What fraction of the image is unshaded?

(8) Find the next number in the sequence.

9, 10, 11, 15, 16, 17, 21, 22, 23, 27, 28, 29, ….

(9) If the width of a rectangle is 161 cm and the perimeter of the rectangle is 9.1 m, then what is the ratio of the width of the rectangle to its length?

(10) An article with price tag of $800 is sold at 20% discount. Due to off-season, the shopkeeper provides an additional discount of 20% on the discounted price. Find the selling price of the article.

Week 3

Choose correct answer(s) from the given choices

(1) Two candles have different lengths and thickness. The shorter lasts 10 hours and the longer 6 hours when both are lit simultaneously. If after 4 hours of their being lit together at the same time, both have the same length, then find the ratio of their original lengths.

a. 5:9                b. 1:2
c. 3:5                d. 6:11

(2) If A * B means (A + B)/2, what is the value of (3 * 3) * 9?
a. 6          b. 4       c. 10        d. 8

(3) If one fifth of a number is 56 less than the original number, find the number.
a. 60          b. 70        c. 75          d. 80

Fill in the blanks

(4) The number of people living in a small town is found to be a perfect cube. We know that the number of men in the town is 63992, and the number of women in the town is 119240. By an odd coincidence, we count and find that the number of children in the town is also a perfect cube. If we give you a hint that this number is more than 32760,then the smallest possible number of children in the town  is ……………..

Answer the questions

(5) Aidan got an average score of 79.25 in 4 tests. He got 80 as the average of the highest 3 scores, and his lowest two scores are the same numbers. What is the average of his highest two scores?

(6) If x² + x – 4 = 0, find the value of x⁴ – 9x² + 22.

(7) There are 5 badges belonging to 5 students. The badges were put into a box, and each student pulls out a badge one after the other. What is the probability that each student gets his or her own badge?

(8) Tiffany wants to print some brochures for her business. If she goes for style 1, it will cost her $163 plus $0.1, per brochure. If she goes for style 2, it will cost her $25 plus $0.4, per brochure. For how many brochures will the price for both the styles be the same?

(9) The number of people living in a small town is found to be a perfect cube. We know that the number of men in the town is 41714, and the number of women in the town is 66548. By an odd coincidence, we count and find that the number of children in the town is also a perfect cube. If we give you a hint that this number is more than 24380, then what is the smallest possible number of children in the town?

(10) Tristan is facing South. He turns 90° in clockwise direction and then turns 45° in anticlockwise direction. Which direction is his back facing now?

Week 4

Choose correct answer(s) from the given choices

(1) Find the value of B from following summation.

a. 0    b. 2     c. 9     d. 1

(2) Two concentric circles are drawn, as shown in the diagram. Concentric circles share the same point as their center. The radius of the smaller circle is one-seventh of the radius of the larger circle. The top half of the larger circle which is outside the smaller circle is shaded. The ratio of the shaded area to the area of the smaller circle in its simplest form is a : b. What are the values of a and b?

a. a = 343 and b = 6
b. a = 1 and b = 49
c. a = 24 and b = 1
d. a = 1 and b = 24

(3) Zachary is facing North. He turns 90° in clockwise direction and then turns 45° in anticlockwise direction. Which direction is his back facing now?

a. North-West       b. South-West
c. South-East       d. North-East

(4) Suppose x − y = 1. Find the value of x⁴ – xy³ – x³y – 3x²y + 3xy² + y⁴.

a. 6            b. 2           c. 3               d. 1

Fill in the blanks

(5) The last two digits of 6105 + 6105² + 6105³ + … + 6105⁶¹⁰⁵ are ………..

Answer the questions

(6) Nur works twice as fast as Tiffany. If Nur can complete the given task in 3 minutes, how long will it take to complete the task when both Nur and Tiffany works together?

(7) Train X takes 42 hours to travel from station A to station B, while train Y takes 7 hours to travel from station B to station A. If train X and Y starts at same time from stations A and B respectively, after what time will they cross each other? (Assume trains travel with uniform speed)

(8) A showroom stocks tiles in combination of 3 colors – Blue, Red, and Orange. 50% of the tiles have white color. 30% of tiles have blue color, and 55% of tiles have red color. No tile has all 3 colors, but some tiles can have 2 colors. What percentage of tiles have only one color?

(9) Ethan reaches his office 1 minute early by traveling at a speed of 25 km/h and reaches 20 minutes late by traveling at a speed of 20 km/h. By how much time will he be early or late if he travels at 30 km/h?

(10) Victoria’s father had a rhombus shaped plot with diagonals of 18 and 36 meters long. He sold the plot and bought a square shaped plot of same area. Find the perimeter of new plot.

Week 5

Choose correct answer(s) from the given choices

(1) There are 400 soldiers and captains in a battalion. If there is one captain for every 9 soldiers, find the numbers of soldiers in battalion.

a. 360         b. 378
c. 342         d. 369

(2) Showing the man in the park, Olivia says, “He is the brother of my uncle’s daughter”. How is Olivia related to the man?

a. Cousin      b. Daughter
c. Aunt          d. Nephew

(3) (-1)⁵⁵⁸⁷ = ?

a. -1            b. 1
c. 5587       d. 0

(4) If we use (x+) to indicate the following sum:

1 + 2 + 3 + … + x

then find the value of k in the following equation:

(10+) – (9+) = (k+).

a. 6       b. 4
c. 2       d. 3

(5) \left( {8888 + \frac{1}{{4444}}} \right)\left( {8888 + \frac{1}{{4444}}} \right) - \left( {8888 - \frac{1}{{4444}}} \right)\left( {8888 - \frac{1}{{4444}}} \right) = ?

a. 4           b. 4444

c. 8888     d. 8

Fill in the blanks

(6) A palindrome number is the same either read from left to right or right to left, for
example, 121 There are ………. 9 – digit palindrome numbers altogether.

Answer the questions

(7) Kate competes in a triathlon in which she has to first swim, then bike, and then run for the same distance. She swims at a rate of 4 kilometres per hour, bikes at a rate of 25 kilometres per hour, and runs at a rate of 10 kilometres per hour. What is her average speed over the entire race?

(8) There is a sequence of numbers {a_1},{a_2},...\,\,\,where\,\,\,{a_1} = 2,{a_2} = 3,\,\,and\,\,{a_n} = \frac{{{a_n} - 1}}{{{a_n} - 2}}\,\,for\,\,n\ge 3

What is the value of a₇₅₆?

(9) Caleb selects 3 numbers randomly from the following set of 5 numbers 4, 5, 2, 6 and  8.

He puts them in the form of a proper fraction of the type a\frac{b}{c}.

What is the probability that you will get a fraction greater than 2\frac{21}{22}.

(10) If a number is divided by 5, remainder is 4. What should be the last digit of the number?

Week 6

Choose correct answer(s) from the given choices

(1) Simplify:

\frac{{\left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)\left( {1 - \frac{1}{{{4^2}}}} \right)...\left( {1 - \frac{1}{{{{9457}^2}}}} \right)}}{{\left( {1 - \frac{1}{{{2^{}}}}} \right)\left( {1 - \frac{1}{{{3^{}}}}} \right)\left( {1 - \frac{1}{{{4^{}}}}} \right)...\left( {1 - \frac{1}{{{{9457}^{}}}}} \right)}}

a. 8809        b. 8227
c. 9457        d. 4729

(2) Aaron has two planks of wood. One of them is 24 m less than 4 times the length of the other one. The two planks put together are 26 metres long. What is the length (in metres) of the shorter plank?

a. 9        b. 8
c. 7        d. 10

(3) There are two numbers such that their product is 27 and sum of the numbers is 12. Find the sum of their squares.

a. 99      b. 89
c. 91      d. 90

Fill in the blanks

(4) The number of

which can fit in the given shape are ……..

(5) For any four numbers p, q, r and s, the mathematical representation
\left| \begin{array}{l}p\,\,q\\r\,\,\,s\end{array} \right| means p × s – q × r.
If  \left| \begin{array}{l}5\,\,1\\3x\,\,\,4x\end{array} \right|

the value of x = ……..

(6) Let, a, b and c be the lengths of the three sides of a triangle. Suppose a and b are the
roots of the equation x² + 6(c + 3) = (c + 6)x and the largest angle of the triangle is x⁰. The value of  x is ……..

Answer the questions

(7) A basket contains three type of fruits weighing 108/7 kg in all. If 47/7 kg of these are apples, 17/7 kg are oranges and the rest are pears. What is the weight of the pears in the basket?

(8) P(x) is a polynomial such that P\left( {x + \frac{5}{2}} \right) = P(x). if P(20) = 226, find the value of P(35)

(9) In a quadrilateral ABCD, if AB // CD, ∠D = 2∠B, AD = b and CD = a. Find the length of the side AB.

(10) Tristan says, ‘Gabrielle is the wife of the grandson of my mother.’ What is the relation of Tristan with Gabrielle?

Hits: 7